Некоторые аспекты карвингового поворота (Несколько простых формул и важных следствий для тех, кто еще не забыл школьный курс физики)

Александр Каниовский

Дайте мне точку опоры и я поверну...
Архимед

Ниже приведены некоторые замечания относительно техники карвингового поворота. Если вас не интересуют научные объяснения, можете сосредоточится только на специально выделенных важных следствиях. Правда в этом случае вам придется принимать их на веру.

Радиус поворота.

Радиус окружности, наилучшим образом описывающей форму бокового выреза лыжи используется производителями лыж для описания геометрии той или иной модели. Однако на практике при резаном скольжении лыжи поворачивают с радиусом значительно меньшим, чем собственный радиус бокового выреза. Связано это с тем, что закантованная и загруженная лыжа прогибается таким образом, что опорный кант оказывается прижатым к склону по кривой, радиус кривизны которой всегда меньше, чем собственный радиус бокового выреза лыжи. Для того чтобы оценить, как угол закантовки влияет на радиус поворота. Рассмотрим, как прогибается по дуге закантованная лыжа:

Для того, чтобы определить радиус кривизны прогиба закантованной лыжи достаточно рассмотреть условия для трех точек на боковом вырезе лыжи: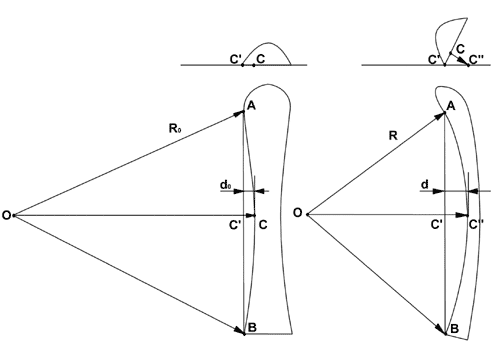
A - носок
B - пятка
С - середина лыжи.
На рисунке утрированно изображена лыжа - вид сверху.

Пусть L - длина канта между точками А и В, а d₀ - глубина бокового выреза.

Тогда R₀ - радиус бокового выреза лыжи может быть найден из соотношения:

Поскольку для любой нормальной лыжи L >> d₀.

Соответственно первая формула может быть переписана в виде:

Или

Теперь посмотрим, что произойдет, если лыжа будет закантована под углом a.

В верхней части рисунка изображена лыжа, закантованная под углом a, но не прогнутая по дуге. В этом случае лыжа касается склона в точках A и B, а точка С висит в воздухе. Теперь прикладываем к лыже усилие необходимое для того чтобы прогнуть ее по дуге, сохраняя заданный гол закантовки. Лыжа будет прогибаться, пока не коснется склона в точке С". Рассмотрим образовавшийся прямоугольный треугольник С"CC'. Собственно нас интересует его гипотенуза C"C'

Рассмотрим, как выглядит ситуация в плоскости склона (нижняя часть рисунка).

Как видно из рисунка, картина полностью эквивалентна рассматривавшейся выше с той только разницей, что в формуле вместо глубины бокового выреза должна стоять глубина прогиба закантованной лыжи d = d₀ / Cos(a).

Соответственно радиус дуги прорезаемой кантом прогнувшейся лыжи будет равен:

Или другими словами

Следствие 3:

Строго говоря, реальный радиус поворота не может уменьшаться до нуля, как это следует из приведенной выше формулы. Во-первых, формула выведена в предположении, что глубина прогиба лыжи много меньше, чем рабочая длина канта. Данное предположение перестает быть верным только при очень больших углах закантовки. Отклонения между реальным радиусом дуги и вычисленным по формуле становятся заметны при углах закантовки превышающих 80 √ 85 градусов. В реальной жизни достичь таких углов закантовки практически невозможно.

Другое ограничение на уменьшение радиуса поворота связано с тем, что лыжник не всегда может продавить сильно закантованную лыжу до того, чтобы она легла на склон по всей длине каната. В этом случае лыжа остается висеть, касаясь склона только участками канта в районе носка и пятки. При этом радиус поворота перестает сокращаться. Возникновение подобной ситуации зависит от жесткости самой лыжи, а также от скорости лыжника, так как именно скорость в данном случае определяет величину центробежной силы прогибающей лыжу. Сегодня современные лыжи стали намного мягче, и даже любителю вполне по силам прогнуть закантованную лыжу таким образом, чтобы радиус поворота сократился по отношению к собственному радиусу бокового выреза в 2 - 3 раза.

Все вышеизложенное предполагает, что кривая, прорезаемая на склоне кантом лыжи, описывается окружностью. Однако тот факт, что рассматривавшиеся кривые прогиба, строго говоря, не являются идеальными окружностями, не должен сильно волновать нас, поскольку любая кривая в данном случае может с большой точностью быть аппроксимирована окружностью. Кроме того, идеальная лыжа должна как раз стремиться писать на снегу дугу в виде идеальной окружности, поскольку только по окружности лыжа может скользить не испытывая дополнительных деформаций.

Обратите внимание на то, что требование жесткости склона в Следствии 3 не случайно. В случае, когда склон не может рассматриваться как жесткая, недеформируемая поверхность все вышеизложенные выкладки неверны. В случае катания по мягкому склону радиус поворота определяется не кривой, которую прорезает на склоне кант лыжи, а собственным прогибом лыжи. Продавливая снег, лыжа формирует на мягком склоне некоторое подобие санной трассы и, фактически, скользит по склону, опираясь на снег не кантом, а всей площадью скользящей поверхности. Соответственно, характерным параметром в данном случае становится радиус прогиба лыжи в снегу. Радиус прогиба зависит от жесткости лыжи, веса лыжника, состояния снега, скорости движения. Попытка строго описать физику катания по мягкому склону вряд ли оправдана, поэтому придется ограничиться лишь несколькими качественными замечаниями.

Прогнуть лыжу в снегу значительно труднее чем, продавить закантованную лыжу на жестком склоне. В случае жесткого склона для прогиба лыжи необходимо преодолеть только упругость лыжи, а на мягком склоне кроме этого нужно затратить энергию на то чтобы промять и уплотнить снег под лыжей. Соответственно радиус поворота на мягком склоне будет больше, чем на жестком.

Если резаный поворот на жестком склоне возможен только с радиусом меньшим собственного радиуса бокового выреза лыжи, то на мягком склоне теоретически возможен резаный поворот с достаточно большим радиусом.

Если, увеличивая угол закантовки на жестком склоне, можно теоретически выполнить резаный поворот очень малого радиуса (поскольку радиус поворота ведет себя как косинус угла закантовки), то в случае резаного поворота на мягком склоне радиус поворота не может быть меньше радиуса прогиба лыжи в снегу даже при самых экстремальных углах закантовки.

В реальной жизни склоны для массового катания специально готовятся для того, чтобы не быть абсолютно жесткими. При катании здесь реализуется некоторая комбинация двух описанных выше режимов. Однако доминирующую роль при формировании дуги поворота на таком склоне все же играет боковой вырез, и поведение лыж оказывается очень близким к поведению лыж на идеально жестком склоне.

Равновесие в повороте.

Рассмотрим условия равновесия горнолыжника в карвинговом повороте на жестком склоне. Очевидно, что для поддержания равновесия тело горнолыжника должно отклоняться внутрь поворота. При этом, специфика равновесия горнолыжника в повороте заключена в том, что наклон тела внутрь поворота приводит одновременно к увеличению угла закантовки, и следовательно к сокращению радиуса поворота (см Следствие 3). В этом состоит коренное отличие равновесия горнолыжника от равновесия, например, мотоциклиста в вираже. Мотоциклист задает рулем фиксированный радиус поворота и наклоняясь внутрь уменьшает опрокидывающий момент центробежной силы обретая устойчивое равновесие.

Лыжник в повороте находится в равновесии, если равнодействующая силы тяжести и центробежной силы проходит через точку контакта лыжи со снегом. Суммарный момент сил относительно данной точки равен нулю.

Поскольку точкой приложения обеих сил является центр масс системы лыжник-лыжи, условие равновесия эквивалентно равенству составляющих этих сил, перпендикулярных оси проходящей через ЦМ и точку контакта со снегом.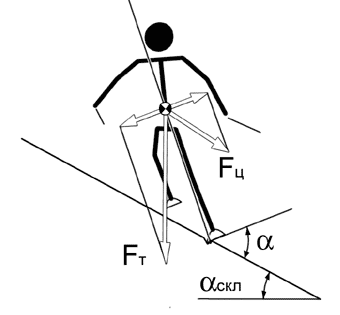

Центробежная сила действующая на лыжника проходящего поворот радиусом R на скорости V:

Сила тяжести действующая на лыжника:

Соответственно условие равновесия лыжника под действием центробежной силы и силы тяжести будет выглядеть следующим образом:

Но как мы знаем из Следствия, радиус поворота зависит от угла закантовки:

И условие равновесия перепишется в виде:

Мы получили необычайно интересный результат. Из уравнения следует, что при достаточно высокой скорости движения лыжник не может достичь бокового равновесия. То, что косинусы в левой части уравнения сократились, отражает тот факт, что при увеличении наклона внутрь поворота момент центробежной силы относительно точки контакта со снегом не уменьшается, как это происходит в случае с мотоциклистом, а остается постоянным. Это происходит потому, что при увеличении угла наклона уменьшается радиус поворота, и, соответственно, возрастает центробежная сила.

Синус в правой части уравнения не может быть больше единицы. Соответственно, нам остается сформулировать следующее следствие:

Следствие 4

Лыжник на лыжах с собственным радиусом R₀ не может стационарно поддерживать равновесие в повороте при движении со скоростью большей или равной:

С учетом угла крутизны склона данное условие для критической скорости можно сформулировать еще жестче:

или:

Чтобы дать вам представление, о каких скоростях идет речь, в таблице посчитано значение критической скорости для некоторых наиболее часто встречающихся у современных моделей лыж радиусов бокового выреза:

Заранее согласен с вами, все выше сказанное звучит несколько непривычно, если не сказать дико. На самом деле ничего страшного не происходит. Тот факт, что равновесие невозможно, означает только то, что вы не можете бесконечно долго резать дугу на данной скорости. Лыжи просто опрокидывают вас в новый поворот, а потом еще и еще, и так до бесконечности. Те, кто уже успел попробовать новые радикальные слаломные модели, наверняка в полной мере успели оценить это потрясающее ощущение, когда не вы едете на лыжах, а лыжи "едут" вас.

Главный вывод, который можно сделать из Следствия 4 состоит в том, что стратегия контроля траектории при катании со скоростями большими и меньшими критической - различны.

Если при катании со скоростями ниже критической доминирующей тактикой является возможность максимально глубоко закрывать дугу поворота, диктуя лыжам момент входа в новый поворот, то в режиме движения со скоростями больше критической процесс поворота переходит в существенно неравновесную моду, когда момент перехода в следующий поворот во многом диктуется динамикой движения по дуге.

С другой стороны, при движении со скоростями, большими критической, лыжник в момент входа в поворот может задавать практически любые углы закантовки, ложась сколь угодно глубоко внутрь новой дуги. В этом случае он гарантирован от ошибок по определению правильного угла наклона корпуса внутрь поворота, поскольку практически любой завал внутрь новой дуги будет компенсирован за счет нарастающей центробежной силы. Соответственно, при таком катании для контроля траектории определяющим будет задание радиуса поворота посредством активного завала тела внутрь нового поворота. Именно так катаются сегодня апологеты радикального карвинга и наиболее техничные представители слаломных дисциплин.

Райан Шоенфельдер в на трассе слалома (комбинация, Олимпиада 2002 Солт Лейк Сити). Классический пример короткого слаломного поворота в исполнении слаломиста новой школы.

Следствие 4 также позволяет сформулировать стратегию подбора инвентаря для катания по подготовленным склонам.

1. Определитесь с характерным для вас радиусом поворота. Исходя из того, что рабочий диапазон радиусов поворота лежит в интервале 0.25 - 0.9 R₀
2. Определитесь со скоростным режимом. Для катания с докритическими скоростями есть смысл остановить выбор на более мягких экспертных моделях с соответствующим R0. Для скоростей больше критической, лучше остановить выбор на спортивных моделях или лыжах для экстремального карвинга. Поскольку, если разогнать до критической скорости лыжу попроще, она может просто сорвать чистое ведение дуги, тем самым автоматически решив проблему с избытком центробежной силы.

В остальном, для катания по подготовленным склонам лыжи стоит подбирать под цвет глаз, комбинезона и ботинок.

Январь 2003
Copyright A. Kaniovsky
shu@hea.iki.rssi.ru